Do you understand this?
Written by David WhiteI was trying to help my 9 year old son with his maths homework last night. Simple, right?
His sums were all division, and not hard, eg 36 divided by 4. He was still struggling though, because he couldn’t explain how he was supposed to work the sums out…my method was all wrong apparently. So it would seem…look what he bought back from school today to ‘help’ him…no wonder so many kids are crap at maths….this is absurd..:

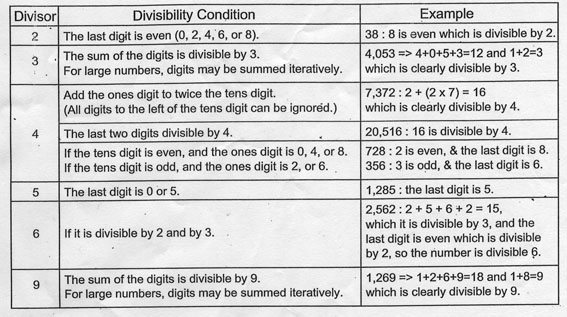
Discussion (10 Comments)
Holy crap. We just learned long division go I guess this was our version
divisor | criterion | example
—————————————————————-
anything | no remainder | 2/2=1 and no remainder so divisible
Boring but easy to remember and applicable to all cases
So they’ve created a whole extra step to help them? Bizarre!
Although I do like the method for figuring out division for higher numbers so you don’t have to waste your time working out the division as a whole (that sentence is nearly as confusing as the table…)
Many years ago I got an A-level in Further Maths and an offer of a place to read Maths at Cambridge (which I turned down, stupidly). This makes no sense to me. Especially the bit that is “clearly divisible by 9”. Nothing clear about that.
We have similar concerns at home with our 5 year old just starting year one. I’m not up to date on new teaching techniques, but it seems like even times tables have been abandoned. Sad thing is that maths is the increasingly the one skill which guarantees a child a successful and creative future. Wish I’d stuck with it – I’d be coding photography apps by now.
Well, that makes me feel less thick. Phew. Times tables do seem to have gone out of the window. Worst thing is I’m unable to help him…
David, I feel the same. I look at that table and I have absolutely no idea what it means.
It basicly states for the numbers…
If it is even, it’s divisible by 2.
If the individual digits add up to a number divisible by 3 (i.e. 642 = 6+4+2 = 12 = 1+2 = 3)
If it ends in 0 or 5, its divisible by 5.
If the invidual digits add up to a number divisible by 3 and it’s even, it’s divisible by 6.
I’m in “Advanced Math” (after Algebra 2, before AP Pre-Calc) and those are the only ones I have ever learned (more as a ‘trick’ from a teacher to help with a quick calc then an actual lesson plan) and they do help over doing long division, just to see if you’ll have a remainder or not.
The 4’s and 9’s make no sense to me though…
The more I think about this the more it annoys me, actually. I was always taught that the most important thing in maths is ‘first principle’. You can’t just tell kids that if all the numbers add up to a multiple of nine it’s divisible by nine, you have to show the proof and help them understand why if they’re going to use it themselves.
I do have vague recollections of being shown these methods – but at secondary school by the quirky, Johnny Ball-like teacher who wore bow ties and filled time by teaching us the maths of bridge and things. In other words, at 14/15 in the context of ‘isn’t it cool that you can do this with numbers’, slightly different when you’re just trying to understand the concept of division…
They left out 42. For which the divisibility condition is “buy a calculator, ffs, because they allow you one in your exam”. Either that or “the meaning of life”. I keep forgetting which, but it may be interchangeable anyway.
Christian – all multiples of 9 add up to 9. So, 18 (1+8), 27 (2+7) 36 (3+6) and so on.
But it’d be more useful to teach them division conceptually, so you link it with multiplication. I knew too many kids when I was “that age” who could do one but not the other. That’s what perplexed me – what kind of teacher has you doing multiplication and division and fails to convey that they’re different directions of the same thing?!?
Although, I’ll confess to looking at this and thinking “oh fuck, this isn’t one of those hypercrazy DoF charts, is it?”
Adam’s right – it’s key to get the kids to understand why division works – providing a list of shortcuts isn’t really teaching. Unfortunately, at times, due to pressure to cover objectives work isn’t always comprehensively taught. Sometimes you get the sense that “it doesn’t matter too much, as long as they get it right in the Yr 6 SATs” Which leaves me – a newly qualified year 5/6 teacher – pretty stressed. Don’t worry: I do force ’em to learn their times tables!